前回、半正多面体の条件について考えた。
無限に存在する角柱と反角柱を半正多面体の対象から除くため、次のような条件にするのが良いのではないかというところまで書いた。
半正多面体の条件(改)
- すべての面が正多角形
- 1つの頂点に集まる面の数と種類が同じ
- ただし角柱と反角柱は除く
しかし、まだ問題があるのである。
その原因が次の多面体だ。
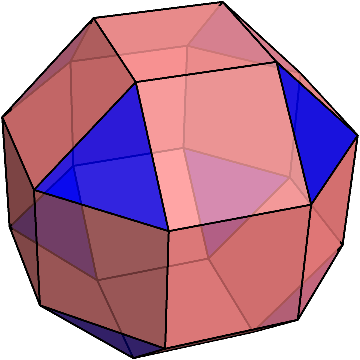
分かりやすくするために正三角形と正方形に違う色をつけた。
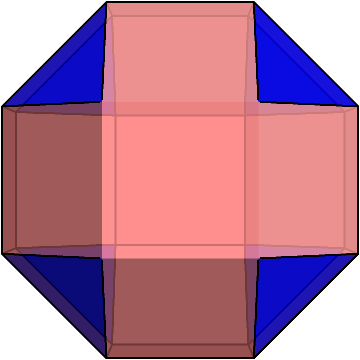
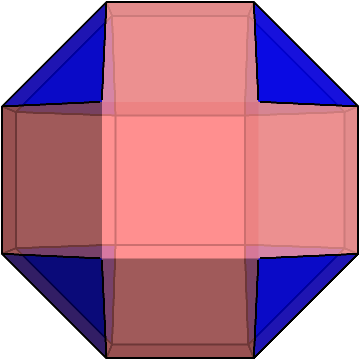
これは、斜方立方八面体という半正多面体の1つで、それぞれの頂点には正三角形が1枚と正方形が3枚ずつ集まっている。
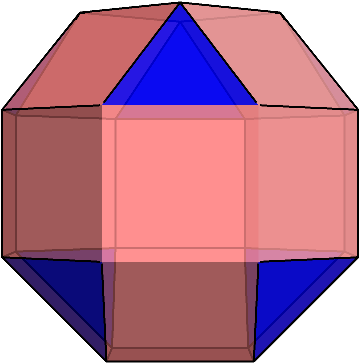
これ自体は綺麗な多面体なのだが、この斜方立方八面体の上半分を45度回転させると別の多面体が出来る。
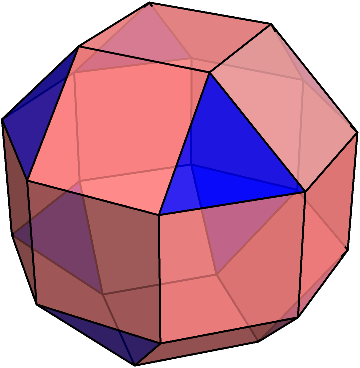
驚くべきことに、この多面体もそれぞれの頂点に正三角形が1枚、正方形が3枚ずつ集まっているのである!
この多面体は、天文学者のケプラーによってすでに発見されていたが、20世紀に多面体の研究をしていたミラーによって再発見されたため、一般的にはミラーの立体と呼ばれている。
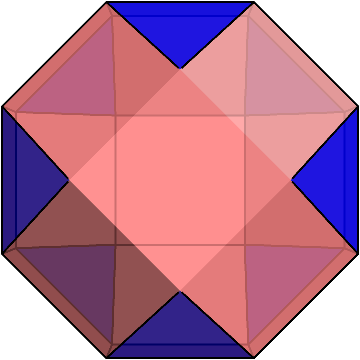
斜方立方八面体とミラーの立体は、パット見では違いが分かりにくいが、正面や真上から見ると違いがよく分かる。
斜方立方八面体
ミラーの立体
というわけで、半正多面体の話に戻ると、今回の冒頭で定義した半正多面体の条件(改)のままだと、このミラーの立体も半正多面体に入ってしまう。
そして、ミラーの立体は、上半分だけを45度回転させた関係上、他の半正多面体に比べると対称性が低くなってしまっている。
ようするに仲間はずれなのである。
そこで、一般的にはミラーの立体も半正多面体からは抜いてしまうことになっている。
さて、これでやっと半正多面体の定義が定まった。
半正多面体の条件(FINAL)
- すべての面が正多角形
- 1つの頂点に集まる面の数と種類が同じ
- ただし角柱と反角柱とミラーの立体は除く
この条件を満たす半正多面体は13個ある。
これらについては次回以降紹介していく。
今回はここまで!