正多面体の1種類の正多角形で出来ているという制限を緩くすることで、アルキメデスの立体と呼ばれる13種類の多面体が得られる。
これらは、「半正多面体」と呼ばれることもあるのだが、一昔前の本や文献を見ると、「準正多面体」と書かれていることが多い。
どちらが正しいのか、この記事で明らかにしておく。
アルキメデスの立体にあたる13種類の多面体は、英語ではsemi-regular polyhedronと書く。
“semi-“の接頭辞は「半-」と翻訳するのが一般的なので、結論としては「半正多面体」が正しいことになる。
しかし、なぜか一時期は「準正多面体」の方が広まってしまったのである。
これに関して、自分が誤訳の原因になったのではないか?とおっしゃっている宮崎興二さんのコラムがあるので紹介しておきたい。
https://web.archive.org/web/20180709064612/https://www.zome.jp/column/clm7/clm7.html
(2020年9月1日現在、Webサイトの証明書の有効期限が切れてしまっており普通には読めなくなっているのでInternet Archiveのリンクを貼っておく)
私としては、昔から読んできた本では皆「準正多面体」が使われていたので、「半正多面体」の表記を見ると未だに少し違和感を覚える。
しかし、半正多面体が正しい訳だということなので、今後は半正多面体の表記を使うのが正しい態度だろう。
というわけで、このブログでも「半正多面体」を採用することにする。
ちなみに、準正多面体に対応する英語はquasi-regular polyhedronになる。
こちらはこちらで定義されていて、半正多面体には頂点の見分けがつかないという条件だったのに対し、準正多面体では頂点だけでなく辺の見分けもつかないという条件が追加されている。
その条件を満たす多面体は2つあり、立方八面体と二十・十二面体だけである。
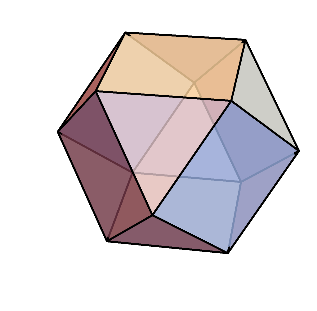
立方八面体 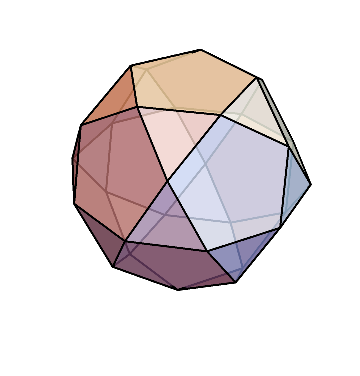
二十・十二面体
今回は、13種類のアルキメデスの立体に相当するのは「半正多面体」であり、「準正多面体」は2種類だけということについて述べた。
今回はここまで!