今回から、多面体に関する記事を書いていく。
最初ということで、まずは僕の一番好きな多面体から紹介したい。
菱形十二面体である。
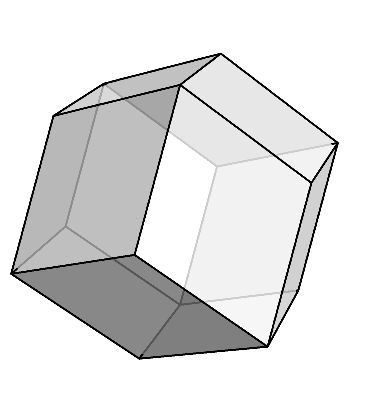
その名の通り、菱形が12枚集まることで構成されている。
頂点の座標表示の一例を挙げると、(±1, ±1, ±1), (±2, 0, 0), (0, ±2, 0), (0, 0, ±2)の計14点である。
ただし、±は取りうる全ての組み合わせを取るものとする。
例えば、(±1, ±1, ±1)は±が3個あるので、合計8頂点を表している。
この座標表示から、菱形の形状を知ることができる。
菱形のうち一枚だけに着目しよう。
例えば、(2, 0, 0), (1, 1 ,1), (0, 2, 0), (1, 1, -1)の4点からなる菱形がある。
この対角線の長さを計算すると、(1, 1 ,1)と(1, 1, -1)の間の距離は2で、(2, 0, 0)と(0, 2, 0)の間の距離は2\sqrt{2}である。
つまり、対角線の長さの比が1 : \sqrt{2}となっている。
この1 : \sqrt{2}という比率は、白銀比と呼ばれており、コピー用紙の縦横の比など、身近にもよく現れる、美しいとされている比率である。
そのため、この菱形のことを白銀菱形と呼ぶ。
菱形十二面体には、数々の面白い性質があるので、次回以降そちらも紹介していきたいと思う。