前回、菱形十二面体の内部には立方体が隠れていると書いた。
今回は、立方体以外の部分に注目したい。
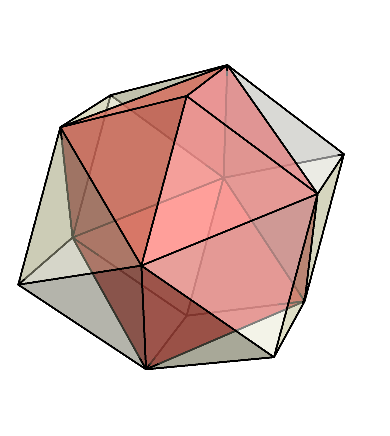
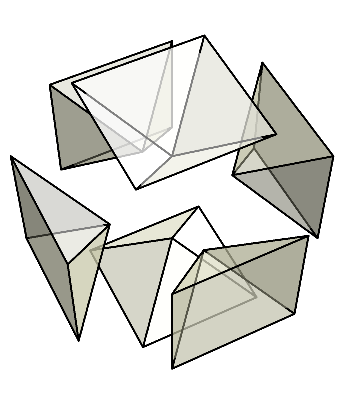
下の図のように、立方体以外の部分は、6個のピラミッドに分かれている。
これら6個のピラミッドを集めてみよう。
すると、再び立方体が現れる。
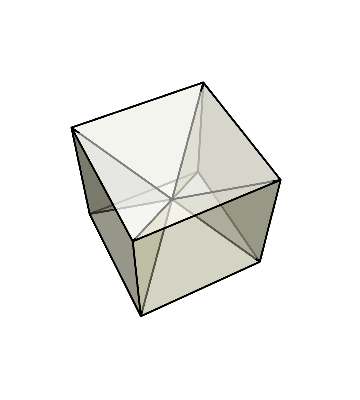
この立方体は、最初に菱形十二面体の内部に隠れていた立方体と全く同じ大きさである。
したがって、菱形十二面体をカットしてできた6個のピラミッドを集めると、同じ大きさの立方体2個を作ることができる。
Science, Mathematics, Polyhedron, etc.
投稿日:
前回、菱形十二面体の内部には立方体が隠れていると書いた。
今回は、立方体以外の部分に注目したい。

下の図のように、立方体以外の部分は、6個のピラミッドに分かれている。
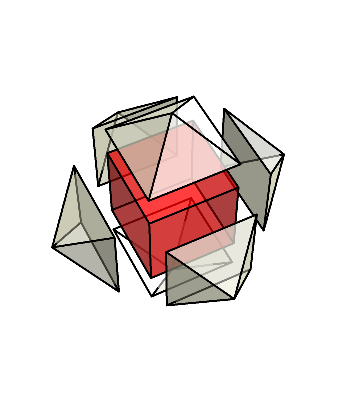
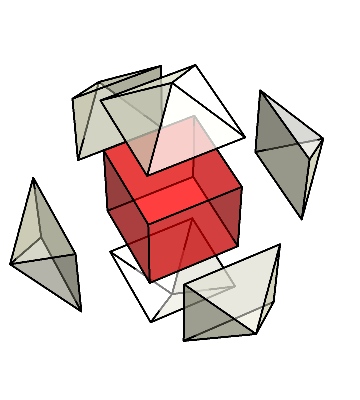
これら6個のピラミッドを集めてみよう。
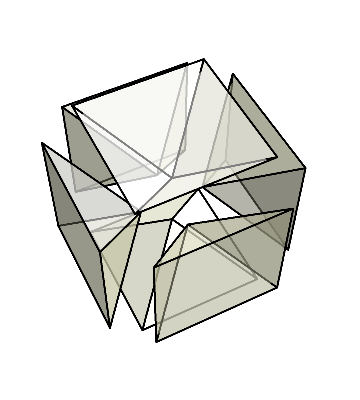
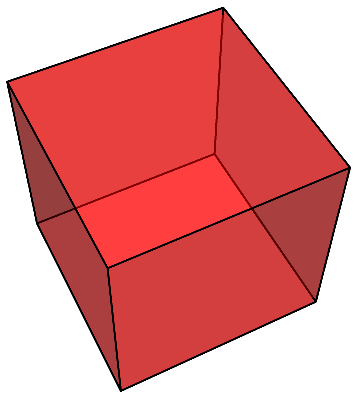
すると、再び立方体が現れる。

この立方体は、最初に菱形十二面体の内部に隠れていた立方体と全く同じ大きさである。
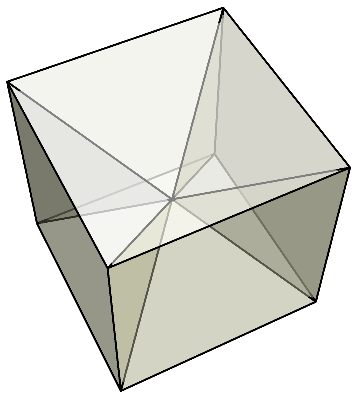
したがって、菱形十二面体をカットしてできた6個のピラミッドを集めると、同じ大きさの立方体2個を作ることができる。
執筆者:epsilon
関連記事
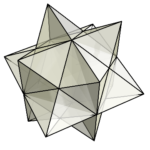
菱形十二面体菱形十二面体 その2菱形十二面体 その3菱形十二面体 その4 今回も菱形十二面体の話をしよう。 その3で、菱形十二面体は立方体とピラミッド6個にカットできることを書いた。 このピラミッド6 …
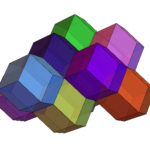
これまでの記事↓菱形十二面体菱形十二面体 その2菱形十二面体 その3菱形十二面体 その4菱形十二面体 その5菱形十二面体 その6菱形十二面体 その7 今回は、菱形十二面体の空間充填について話をしよう。 …

前回、投影と呼ばれる、3次元の物体を2次元に描き表すための方法を紹介した。 この投影とはいったいどういう操作なのか、数学を用いて解説してみようと思う。 まず、キャビネット図を例にとって考えてみよう。 …