前回、立方体の辺をカットしていくことを考えた。
今回は、同じことを正八面体に対してやってみよう。
前回のMathematicaの式を少しいじるだけでそれが可能になる。
RegionPlot3D[Abs[x + y + z] <= 1 && Abs[-x + y + z] <= 1 && Abs[x - y + z] <= 1 &&Abs[x + y - z] <= 1&&Abs[x + y] <= a && Abs[x - y] <= a && Abs[y + z] <= a && Abs[y - z] <= a && Abs[x + z] <= a && Abs[x - z] <= a, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Mesh -> None, PlotPoints -> 100]
前回の関数との違いは、大かっこの中の最初の4つの式である。
x+y+z, -x+y+z, x-y+z, x+y-zの絶対値が1以下という条件を加えることで、正八面体を用意した。
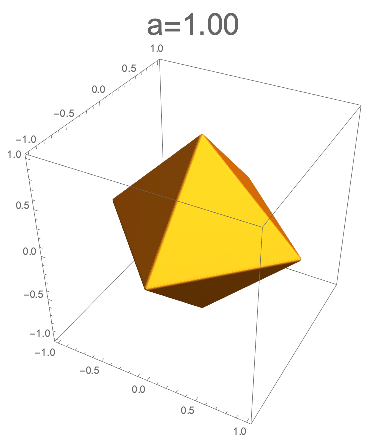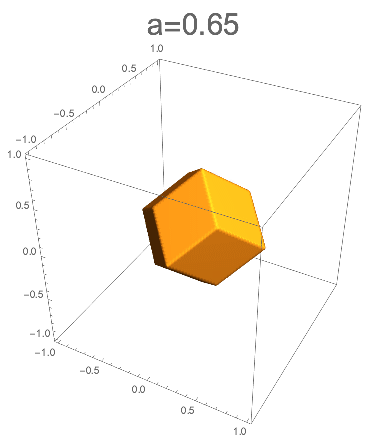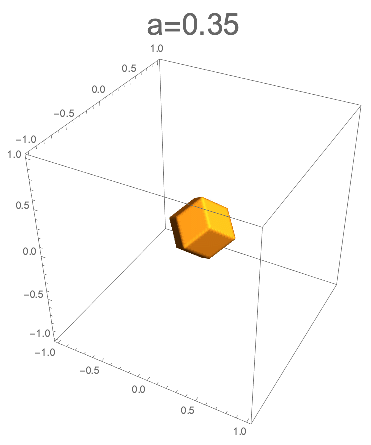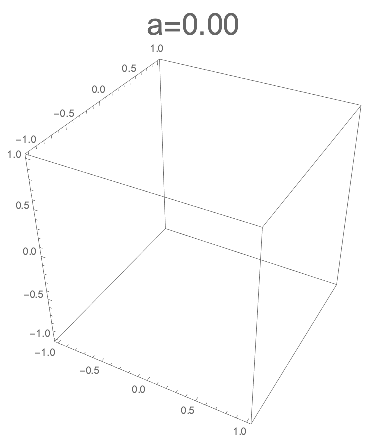
今回は、a=1から始めて小さくしていく。
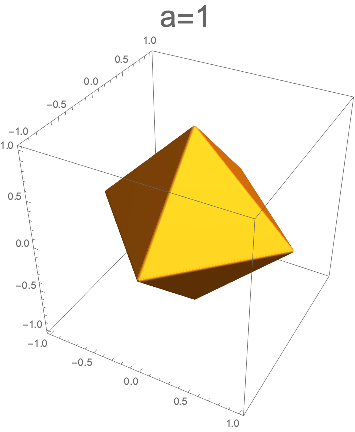
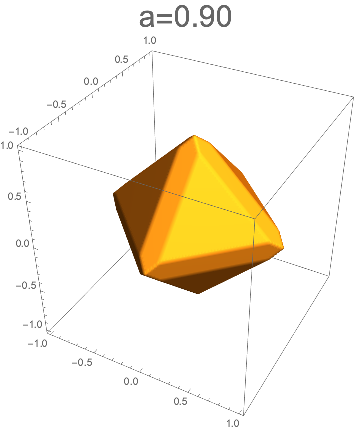
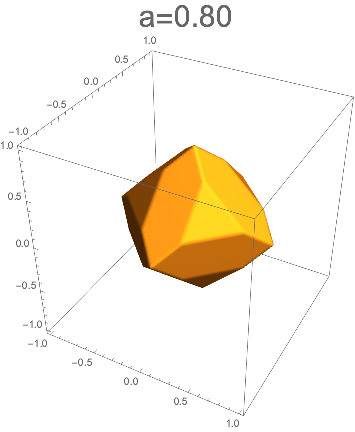
aが1を切ると、辺がカットされ始める。
ここで現れた多面体は、切稜八面体と呼ばれる。
正三角形が8枚と細長い六角形が12枚あり、18面体となっている。
ここでの「稜」とは、角や隅のことを指す漢字で、数学的には平面と平面が交わるところを指す。
多面体で平面と平面が交わるところと言えば辺のことなので、切稜というのはそのままの意味で辺をカットすることを指している。
実は、古今東西さまざまな多面体を見たり作ったりしてきた筆者だが、この切稜八面体はあまり知らなかった。
いずれ模型を作って手にとってみたいと思っている。
さて、a=0.7のときにはほとんど三角形の部分はなくなり、菱形十二面体が現れる。
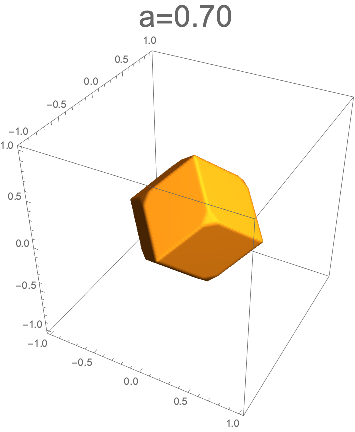
さらにaを小さくしていくと、あとは立方体のときと同じように菱形十二面体の形を保ったまま小さくなっていく。
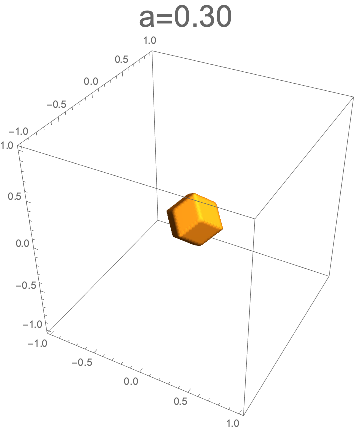
今回の内容もgifアニメにしたのでぜひ見てもらいたい。