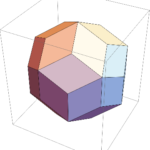
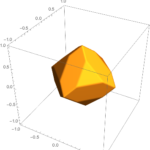
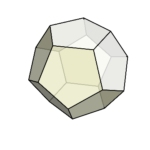
アユイ構成(Häuy Construction)という多面体の構成法がある。
この考案者のルネ=ジュスト・アユイは、18世紀のフランスの鉱物学者で、「鉱物学の父」と呼ばれている。
アユイは「結晶は小さなユニットの集まりで出来ている」という理論を提唱した。
その一例がアユイ構成である。以下でそれを紹介しよう。
アユイ構成では、多面体を立方体の集まりによって表現する。
一番簡単な例として、立方体を積み上げてピラミッドを作ることを考えよう。
9個の立方体を正方形状に並べて、その中心に1個立方体を積み上げると、次のように小さいピラミッドができる。

底面となる正方形をもっと大きくして、そこから階段状に積み上げていけば、次のようにしてより大きいピラミッドを作っていくことができる。
使う立方体の数をより多くしていけば、形はどんどん四角錐に近づいていく。

これは10段のときのピラミッドである。
さて、使った立方体の数を計算してみよう。
ピラミッドの段数をnとすると、使った立方体の数は
1^2+3^2+5^2+...+n^2となるので、Σを使って表して計算すると、
\sum_{k=1}^{n} (2n-1)^2 \\ = 4 \sum_{k=1}^{n} k^2 - 4 \sum_{k=1}^{n} k + \sum_{k=1}^{n} 1 \\ = 4\frac{n(n+1)(2n+1)}{6} + 4\frac{n(n+1)}{2} + n \\ = \frac{n(4 n^2 - 1)}{3}となる。
n=1, 2, 3,…を代入してみると、
1, 10, 35, 84, 165, 286, 455, 680, 969, 1330, ...となる。したがって、先ほどの10段のピラミッドでは1330個の立方体が使われていたことが分かった。
菱形十二面体の話まで進まなかったが、今回はここまで!