前回、アユイ構成という、立方体を使って多面体を近似するやり方を紹介した。
菱形十二面体 その１５
投稿日：2020年8月21日 更新日：
執筆者：epsilon
関連記事
-
-
前々回、前回と、半正多面体の定義について説明した。 今回は、具体的にはどんな半正多面体があるのか紹介する。 半正多面体は、13種類存在し、いくつかのグループに分類することができる。 順番に見ていこう。
-
-
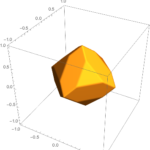
これまでの記事 前回、立方体の辺をカットしていくことを考えた。 今回は、同じことを正八面体に対してやってみよう。 前回のMathematicaの式を少しいじるだけでそれが可能になる。 RegionPl …
-
-
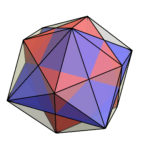
前回に引き続き、菱形十二面体の話をしよう。 前回、頂点座標が(±1, ±1, ±1), (±2, 0, 0), (0, ±2, 0), (0, 0, ±2)で表されることを述べた。 ご覧のように、菱形 …
-
-
正多面体の1種類の正多角形で出来ているという制限を緩くすることで、アルキメデスの立体と呼ばれる13種類の多面体が得られる。 これらは、「半正多面体」と呼ばれることもあるのだが、一昔前の本や文献を見ると …
-
-
今回は、正多面体の制限を少し緩くした、半正多面体についての話をするのだが、その前に正多面体のおさらいをしよう。 正多面体の条件 すべての面が同じ正多角形1つの頂点に集まる面の数が同じ という2つの条件 …
- PREV
- 菱形十二面体 その１４
- NEXT
- 正多面体が５つしかない理由
