今回は正多面体の話をしよう。
正多面体とは、
すべての面が正多角形で、1つの頂点に集まる面の数が同じ凸多面体
のことである。
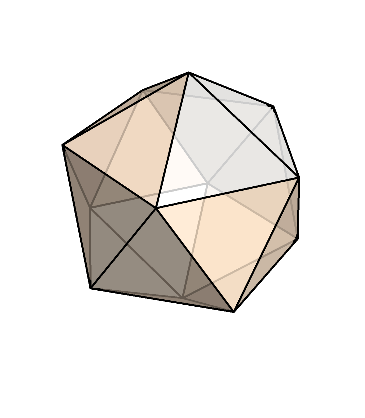
正多面体は、正四面体、正六面体(立方体)、正八面体、正十二面体、正二十面体の5つしか存在しない。
なぜこの5つしかないか。
この疑問に答えるには、1点に集まる面の数と種類に着目すればこの5種類しかないことを証明できる。
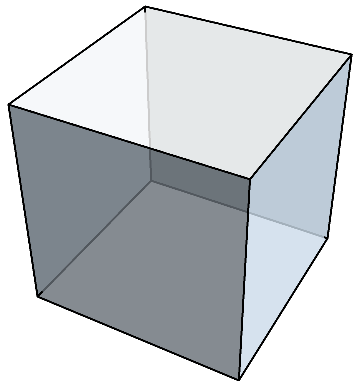
まず、正方形から作られる正多面体について考えよう。
正方形を使う場合、1つの頂点に集まる正方形の数は3枚でなければいけない。
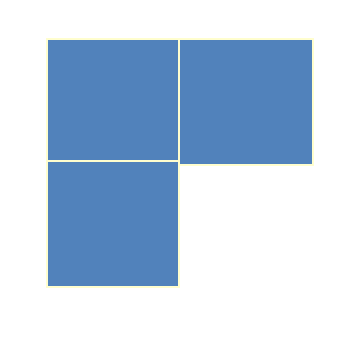
2枚だと立体にならないし、4枚だと360度になってしまい、折りたたむ前に平面になってしまうからである。
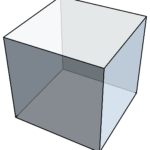
1つの頂点に正方形が3枚ずつ集まるようにしながら正方形を集めていくと、立方体が組み上がる。
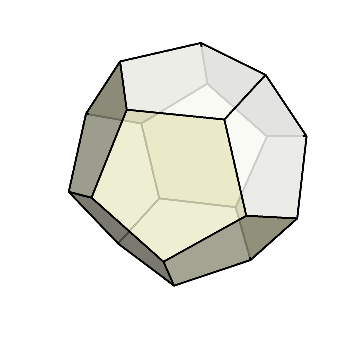
正五角形を使う場合も、やはり1つの頂点に集まるのは3枚でなければいけない。
4枚以上では組み上げる前から360度を超えてしまうからである。

このとき、正十二面体が出来る。
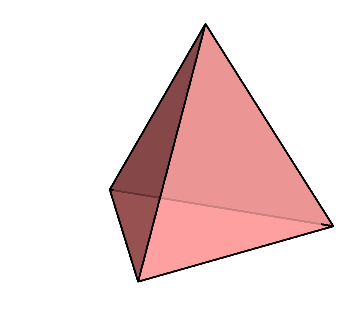
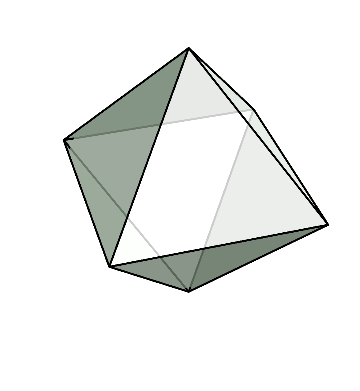
最後に、正三角形によって出来る正多面体には何があるか考えよう。
正三角形の場合、1つの頂点に3から5枚集めることが出来る。
6枚以上だとやはり360度以上になってしまう。
それぞれ、正四面体、正八面体、正二十面体が出来上がる。
最後に、正六角形以上は使えないか考えよう。
正六角形を3枚集めると360度になってしまい、立体にすることができない。
正七角形以上では360度を超えてしまい、やはり不可能である。
以上より、正多面体は5つしかないことが証明された。
2次元だと正多角形は無限にあるのに、3次元になると急に5つだけになってしまうのである。
今回はここまで!