私は今までの多面体の記事を書くにあたってMathematicaというソフトを利用しているのだが、Mathematicaの機能にはかなり便利なものもあって、その一つを使ってみたので紹介する。
実は、有名な多面体のデータは最初から含まれており、それを呼び出すだけで画像を生成できる。
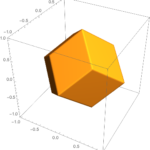
例えば、PolyhedronData["RhombicDodecahedron"]と書くだけで、次の画像が得られる。
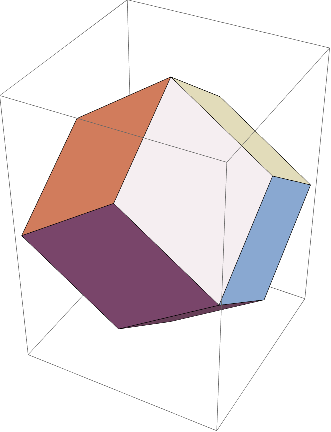
これは菱形十二面体だが、RhombicDodecahedronの部分をRhombicTriacontahedronとすれば、菱形三十面体が得られる。
この多面体はまだ紹介していないが、いずれ記事でも詳しく説明したいと思う。
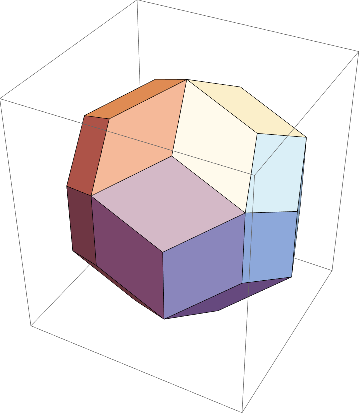
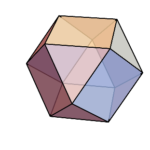
他にも、RhombicIcosahedronとすれば、菱形三十面体の一部の面を取り除くことによって得られる、菱形二十面体の画像が作れる。
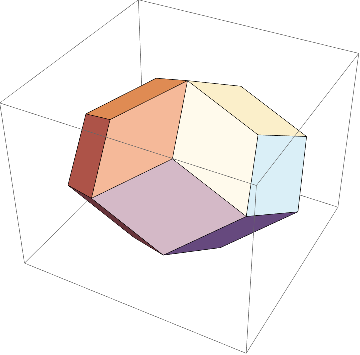
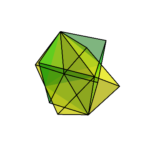
また、次の多面体は星型をしており、菱形六十面体と呼ばれている。
これはRhombicHexecontahedronとすれば良い。
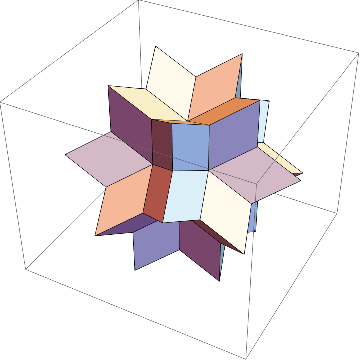
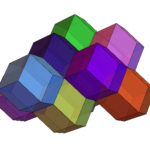
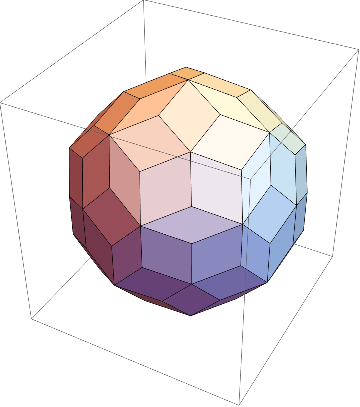
最後に、菱形九十面体である。
描くにはRhombicEnneacontahedronとする。
これは今までとは違い、2種類の菱形からできている。
以上、いろいろな菱形多面体たちを紹介してきた。
今回はここまで!