これまでの記事↓
菱形十二面体
菱形十二面体 その2
菱形十二面体 その3
菱形十二面体 その4
菱形十二面体 その5
菱形十二面体 その6
菱形十二面体 その7
今回は、菱形十二面体の空間充填について話をしよう。
空間充填とは、その名の通り、空間内を図形で隙間なく埋め尽くすことを指す。
一番簡単な空間充填の例は、立方体を積み重ねたものである。

この図では10個程度しか積み重ねていないが、空間充填と呼ぶためには無限に埋め尽くすことができることが分かっていなければいけない。
しかし図の積み重ね方を延長して立方体を無限に埋め尽くしていくことが出来ることはすぐ分かるだろう。
実は、菱形十二面体も空間充填が可能な多面体なのである。
充填の仕方は単純で、菱形の面同士をくっつけていくだけで良い。
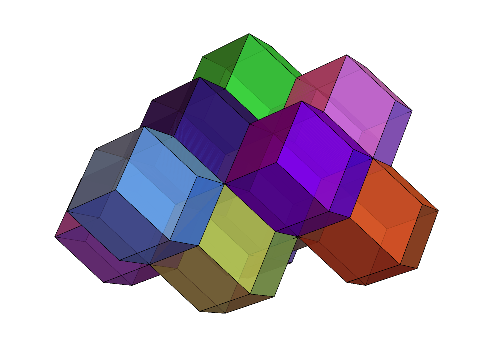
空間充填したときの菱形十二面体同士の位置関係は、球をできるだけ隙間が少なくなるように詰めたとき(最密充填と言う)の位置関係に対応している。
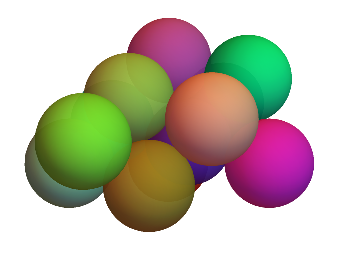
ちなみに、立方体と菱形十二面体以外に空間充填できる多面体としては、
- 三角柱
- 六角柱
- 切頂八面体
が知られている。
切頂八面体とは、正八面体の先を切り落として出来る多面体で、半正多面体のひとつである。
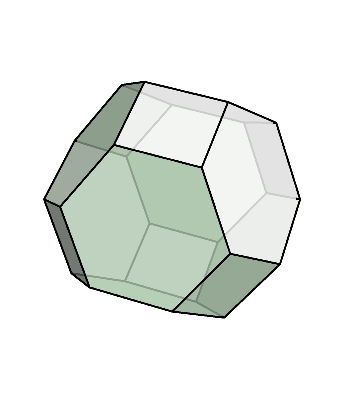
このように、切頂八面体は正方形と正六角形で出来ている。