前回に引き続き、菱形十二面体の話をしよう。
前回、頂点座標が(±1, ±1, ±1), (±2, 0, 0), (0, ±2, 0), (0, 0, ±2)で表されることを述べた。
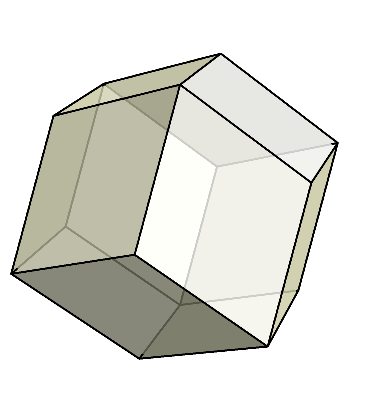
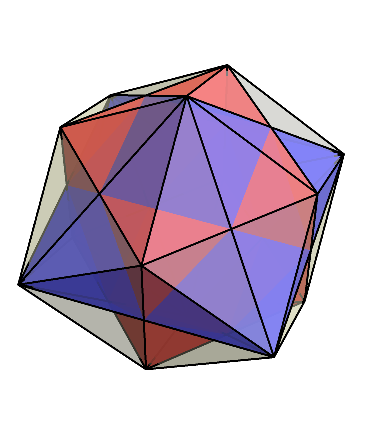
ご覧のように、菱形十二面体には、菱形の鋭角が4つ集まっている頂点と、菱形の鈍角が3つ集まっている頂点の2種類がある。
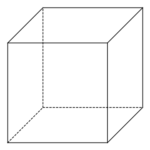
このうち、菱形が3つ集まっている頂点だけを結ぶと、なんと内部に立方体が現れる。
頂点座標で言うと、(±1, ±1, ±1)の8点である。
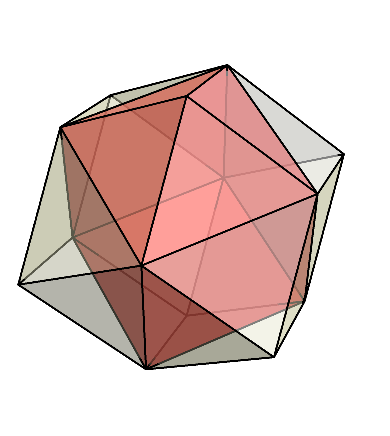
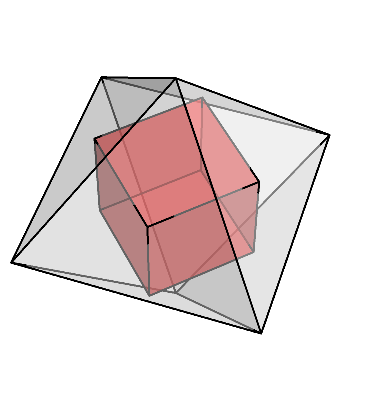
今度は、菱形が4つ集まっている頂点だけを結ぶと、内部に正八面体が現れる。
こちらは頂点座標で言うと、(±2, 0, 0), (0, ±2, 0), (0, 0, ±2)の計6点である。
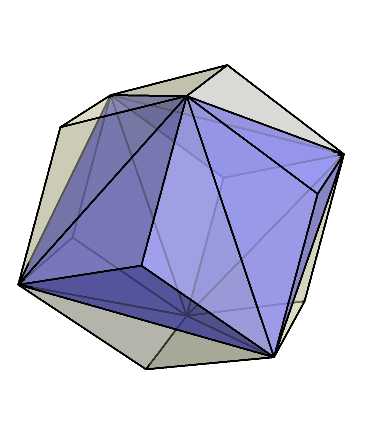
この菱形十二面体の内部に現れた立方体と正八面体は、お互いに貫きあっていて、辺同士がそれぞれの中点で交わっている。
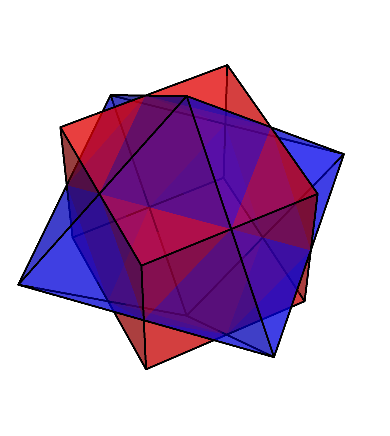
この立方体と正八面体が貫きあっている図は、複合多面体と呼ばれるものの一種である。
このように綺麗な図が描けるのは、立方体と正八面体が双対の関係にあるからである。
双対については多くの例を挙げていずれ詳しく書くつもりだが、一言で言うと面の中心を頂点に対応させ、逆に頂点を面に対応させる変換のことである。
このように、正八面体の各面の中心を結ぶと立方体になり、立方体の各面の中心を結ぶと正八面体になる。
最後に、立方体、正八面体、菱形十二面体を同時に書き込んだ図を載せて終わりにしよう。