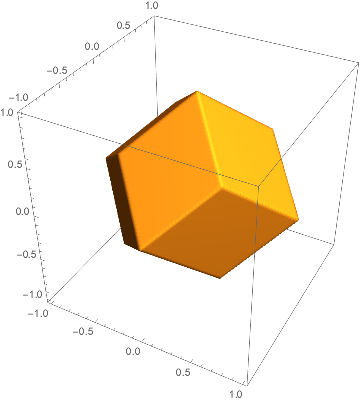
菱形十二面体その12では立方体の辺をカットしたものを考えた。
このとき出てきた次の多面体は、切稜立方体と呼ばれる。

また、その13では正八面体の辺をカットして、切稜八面体が現れた。
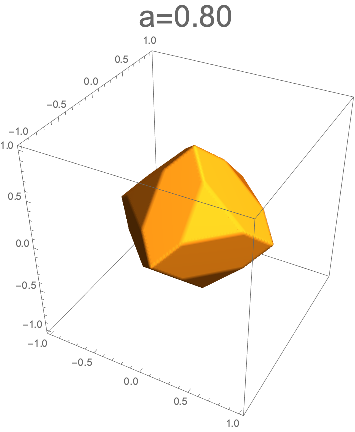
そして、いずれも場合でも、カットする量を増やしていくと、菱形十二面体が現れた。
さて、今回は正四面体の辺をカットしたときにどうなるか見てみよう。
まず、正四面体を準備するには、x + y + z ≦ 1 , -x – y + z ≦ 1 , x – y – z ≦ 1, -x + y – z ≦ 1を全て満たす領域を取ればよい。
そこから、カットする深さを決める定数をaとして、|x| ≦ a, |y| ≦ a, |z| ≦ aを条件に加えれば、正四面体の辺をカットすることができる。
Mathematicaでの関数は次のようになった。
RegionPlot3D[x + y + z <= 1 && -x - y + z <= 1 && x - y - z <= 1 && -x + y - z <=1 && Abs[x] <= a && Abs[y] <= a && Abs[z] <= a, {x, -1, 1}, {y, -1, 1}, {z, -1,1}, Mesh -> None, PlotPoints -> 100]
a=1のときはまだどこもカットされておらず、正四面体のままである。

そこからaを小さくしていくと、徐々に辺がカットされていく。
a=0.5ではかなり六角形が目立つようになってきている。
上の2つや下の多面体など、正四面体の辺をカットすることで出来た多面体を、切稜四面体と呼ぶ。

そして、a=0.35ではほとんど立方体になってしまった。
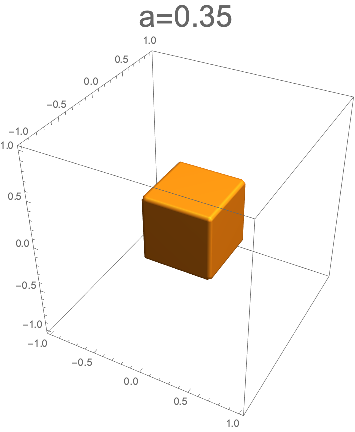
その後は立方体の形を保ったまま小さくなって消える。
正四面体の辺をカットすることで別の正多面体である立方体が中から現れてくるのは興味深い。
これで、正多面体5つのうち、正四面体、立方体、正八面体の切稜を行った。
残り2つ、正十二面体と正二十面体が残されているが、これは別の機会にやってみることにしよう。
今回の話もgifアニメにしたのでぜひ見てもらいたい。

今回はここまで!