今回は、Mathematicaで領域をプロットする機能を使って菱形十二面体に関係する話をしよう。
Mathematicaには、不等号で表される領域をプロットするための関数が用意されている。
2次元の場合はRegionPlot、3次元の場合はRegionPlot3Dという関数である。
今回は、RegionPlot3Dの方を使う。
使い方は、Mathematica公式のページが詳しいのでそちらを見るのが早いが、基本的には
RegionPlot3D[(領域を表す不等式), {x, xの最小値, xの最大値}, {y, yの最小値, yの最大値}, {z, zの最小値, zの最大値}]
とすれば良い。
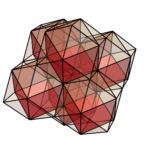
さて、唐突だが、立方体の全ての辺をカットすることを考えたい。
この操作は、RegionPlot3Dを使えば簡単にできる。
まず、立方体を用意する。
そのためにはRegionPlot3Dにおいて、x, y, zの最小値と最大値をそれぞれ同じにすれば良い。
今回は最小値を-1、最大値を1とした。

次に、辺をカットするのだが、例えば+x, +y方向の辺をカットするには、x+y≦a (aは定数)とすれば良い。
辺は全部で12個あるので、x-y≦a, y+z≦a, …と順に条件を追加すれば良い。
今回はより簡単に記述するためにx+y, x-y, y+z, y-z, x+z, x-zのそれぞれの絶対値が定数以下になるという条件を付け加えた。
最終的に、描画のための関数は次のようになった。
RegionPlot3D[Abs[x + y] <= a && Abs[x - y] <= a && Abs[y + z] <= a && Abs[y - z] <= a && Abs[x + z] <= a && Abs[x - z] <= a, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Mesh -> None, PlotPoints -> 100]
ここでは、描画する点の数を増やして滑らかに描けるようにした。
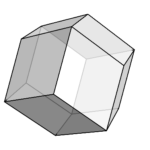
aが2以上のときは立方体のままなので、この関数を使って、aの値を2から少しずつ小さくしていく。
上はそれぞれa=1.9、a=1.8のときである。
さらに小さくしていくと、a=1.3あたりでは切頂八面体のようになり(正確には違う)、

a=1でついに菱形十二面体が現れる。
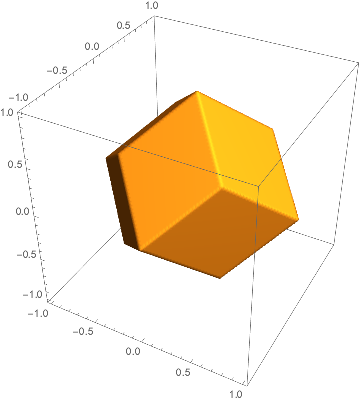
それ以降は菱形十二面体の形を保ったまま、小さくなっていく。
下はa=0.5のときである。

今回の内容をgifアニメーションにしたのでぜひ見てもらいたい。