前回、菱形十二面体による空間充填が可能なことについて書いた。
今回はこれをもう少し掘り下げてみる。
そのために、菱形十二面体について話をする前に、いったん平面充填についての話をしよう。
空間充填が多面体で3次元を埋め尽くすものだったのに対し、平面充填は多角形で2次元を埋め尽くす。
例えばパッチワークは平面充填の一例である。

一番単純な平面充填は、正方形によるものである。

ここに、次のように市松模様になるように数ある正方形のうちの半分にその正方形の対角線を書き込む。

すると、見方を変えると、下図のような斜め向きの赤い正方形が無数に出来ており、赤い正方形による平面充填になっている。
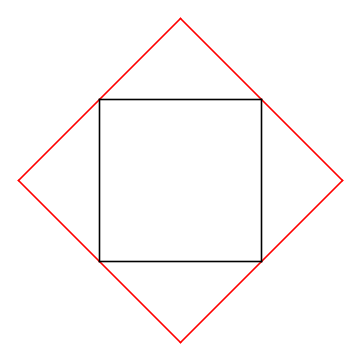
この赤い正方形は元の黒い正方形の2倍の面積を持つ。
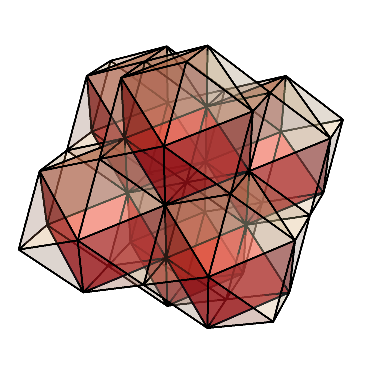
さて、この操作を立方体の空間充填に対して行うとどうなるだろうか。
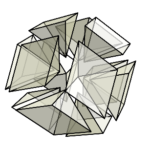
立方体の空間充填に対して、市松模様状になるように、立方体のうち半分を6つのピラミッドに切り分ける。
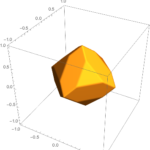
すると、このように菱形十二面体の空間充填が浮かび上がってくる。
間に少し空間を開けてみて、一部分だけ描写したものがこちらである。
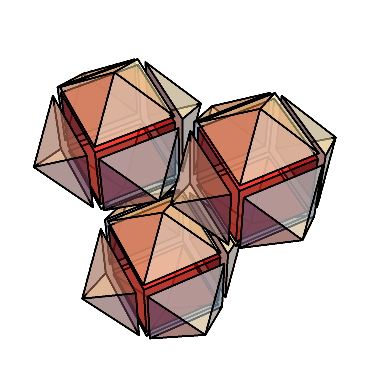
正方形のときはこの操作を行って出来るのは面積が2倍の正方形だったが、立方体のときには大きい立方体が出来るのではなく、菱形十二面体が出来た。
そして、それはそのまま菱形十二面体の空間充填を表している。