前回、菱形十二面体の内部には立方体が隠れていると書いた。
今回は、立方体以外の部分に注目したい。
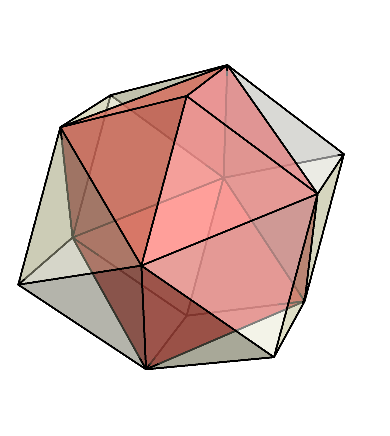
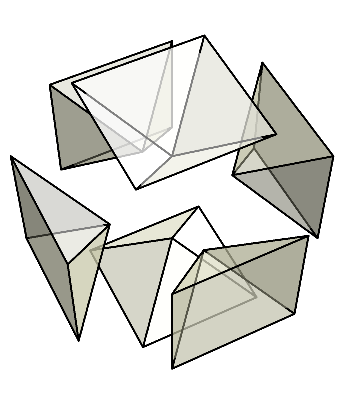
下の図のように、立方体以外の部分は、6個のピラミッドに分かれている。
これら6個のピラミッドを集めてみよう。
すると、再び立方体が現れる。
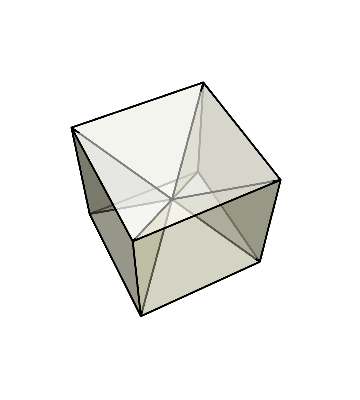
この立方体は、最初に菱形十二面体の内部に隠れていた立方体と全く同じ大きさである。
したがって、菱形十二面体をカットしてできた6個のピラミッドを集めると、同じ大きさの立方体2個を作ることができる。
Science, Mathematics, Polyhedron, etc.
投稿日:
前回、菱形十二面体の内部には立方体が隠れていると書いた。
今回は、立方体以外の部分に注目したい。

下の図のように、立方体以外の部分は、6個のピラミッドに分かれている。
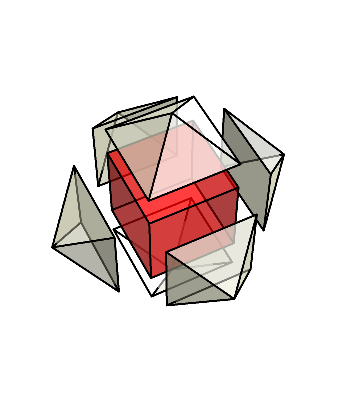
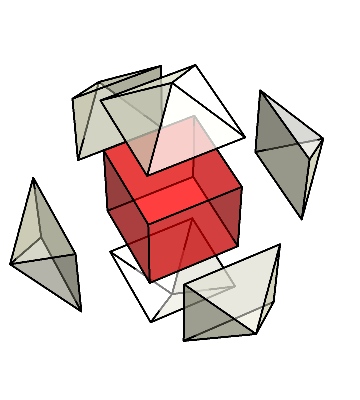
これら6個のピラミッドを集めてみよう。
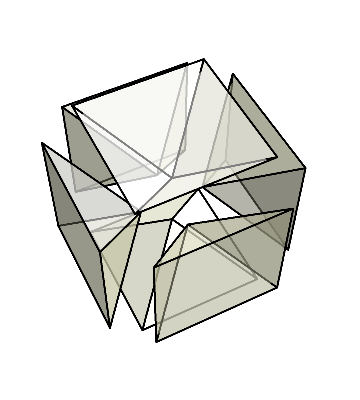
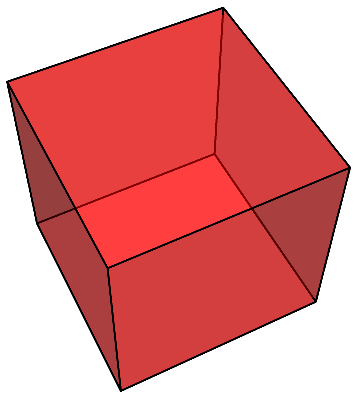
すると、再び立方体が現れる。

この立方体は、最初に菱形十二面体の内部に隠れていた立方体と全く同じ大きさである。
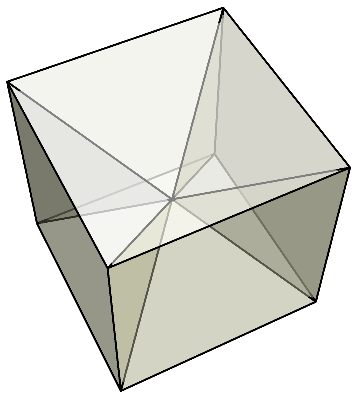
したがって、菱形十二面体をカットしてできた6個のピラミッドを集めると、同じ大きさの立方体2個を作ることができる。
執筆者:epsilon
関連記事
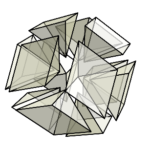
これまでの記事↓菱形十二面体菱形十二面体 その2菱形十二面体 その3菱形十二面体 その4菱形十二面体 その5 今回も菱形十二面体の話をしよう。 今回は、菱形十二面体の各菱形の辺から中心に向かって切って …

これまでの記事 今回は、菱形十二面体の対称性に注目してみよう。 この菱形十二面体を、対称性の高い方向から見てみるとどうなるだろうか。 まず、菱形十二面体には、菱形の鋭角が4枚集まっている頂点と、菱形の …
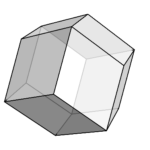
今回から、多面体に関する記事を書いていく。 最初ということで、まずは僕の一番好きな多面体から紹介したい。 菱形十二面体である。 その名の通り、菱形が12枚集まることで構成されている。 頂点の座標表示の …
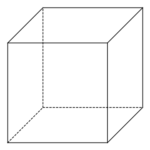
今までに菱形十二面体の記事をたくさん書いてきたが、菱形十二面体についてどうしても書きたいことがある。 それは、「菱形十二面体は4次元立方体の射影である」という事実である。 しかし、これについて書くため …