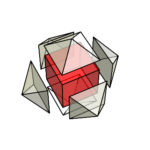
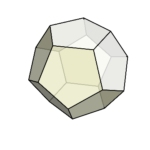
今までに菱形十二面体の記事をたくさん書いてきたが、菱形十二面体についてどうしても書きたいことがある。
それは、「菱形十二面体は4次元立方体の射影である」という事実である。
しかし、これについて書くためには、その前に射影とは何か?という話をしなければいけない。
射影とは、一言で言うと影のことである。
例えば、私たちの身体は3次元の物体だが、地面に映る影は2次元になっており、これは一種の射影である。
実は、射影を使うことで、普通は想像することも難しい4次元の世界を「見る」ことが出来るようになる。
この記事シリーズでは、
- 射影とは何か
- 射影の数学的な説明
- 射影を4次元に適用するとどんなことが分かるようになるのか
といったことを解説していきたいと思う。
まず、3次元のものを2次元に移す射影である、投影について解説しよう。
投影
3次元空間の物体を2次元平面上に書き写すことを投影と呼ぶ。
等角図やキャビネット図といった単語を聞いたことはないだろうか。
これらは投影の方法の例である。
投影では、縦、横、奥行きの3つの直行する軸を平面上でどのように表すかによってその種類が変わる。
等角図は、3つの直行する軸の間の角度をそれぞれ120度ずつとする投影法である。
等角図で描く長さは実際の物体と同じ長さを用いる。
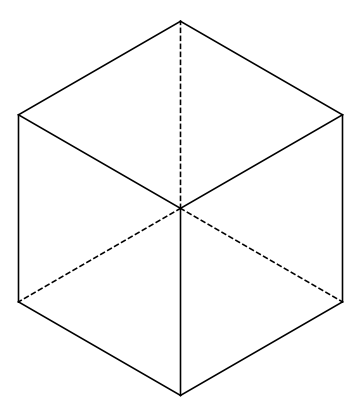
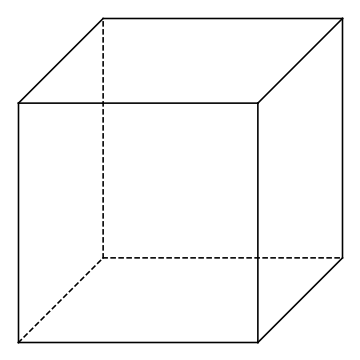
キャビネット図は、縦と横の間の角度を90度としてそのまま描き、奥行きを斜め45度として実際の半分の長さで描く。
今回はここまで!