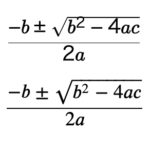前回、1つの頂点に集まる面の種類と数を考えることで、正多面体が5種類しかないということを証明した。
今回は、別の方法で同じことを証明しようと思う。
そのために、次の定理を用いる。
オイラーの多面体定理
穴の開いていない多面体について、次の等式が成り立つ。
(頂点の数) − (辺の数) + (面の数) = 2
今回は証明は省略するが、どんな複雑な多面体についても上の式を計算すれば必ず2になるというのだからなかなか強力な定理である。

(頂点の数) − (辺の数) + (面の数) = 2
になる
さて、正多面体の証明に移っていこう。
すべての面が正N角形となっている正多面体を考える。
1角形や2角形は存在しないので、当然Nは3以上である。
さらに、1つの頂点に集まる面の数をMとする。
前回も書いたように、Mは3以上でなければいけない(でないと立体にならないので)。
最後に、全部の面の数をFとする。
さて、このときに頂点の数・辺の数がN,M,Fを用いてどう表されるか見ていこう。
各面に頂点はN個ずつあるので、頂点はN×F個になる、と言いたいところだが、これは多すぎである。
なぜなら、1つの頂点にM個ずつ面が集まっているからである。
立方体を例にとって考えてみよう。
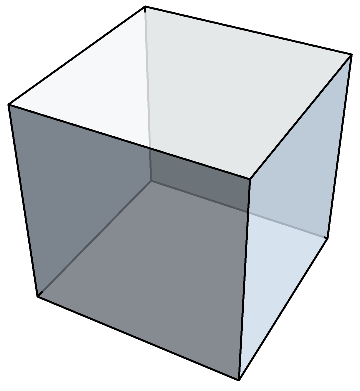
立方体は、6面あり、1つの面に4つ角があるので、頂点が6×4=24あるように思えるが、1つの頂点に3枚ずつ集まっているので、1つの頂点を3度数えてしまっている。
なので、6×4÷3=8が実際の頂点の数である。
同じように考えて、一般に頂点の数はN×FをMで割って、
\frac{NF}{M}で表される。
次に、辺の数を考えよう。
こちらも先ほどと同じように考えると、辺は各面にN個あり、N×Fになりそうだが、一つの辺には2つの面がくっついている。
したがって、一般に辺の数はN×Fを2で割って、
\frac{NF}{2}で表される。
さて、証明の準備が整った。
今までに求めた頂点の数、辺の数、面の数をオイラーの多面体定理に代入すると、
\frac{NF}{M} - \frac{NF}{2} + F = 2となり、これを変形すると、
F = \frac{4M}{(2N+2M-NM)}となる。
さて、面の数Fは自然数なので、分母の(2N+2M-NM) は正の数でなければいけない。つまり、
2N+2M-NM > 0これを変形して、
(N-2)(M-2) < 4が得られる。N≧3、M≧3かつ上の不等式を満たす(N,M)の組は、
(N,M)=(3,3), (3,4), (3,5), (4,3), (5,3)の5通りしかない。
これらの解がそれぞれ、正四面体、正八面体、正二十面体、正六面体(立方体)、正十二面体に対応している。
というわけで、オイラーの多面体定理を用いて正多面体が5種類しかないことを証明した。
今回はここまで!