今回は、正多面体の制限を少し緩くした、半正多面体についての話をするのだが、その前に正多面体のおさらいをしよう。
正多面体の条件
- すべての面が同じ正多角形
- 1つの頂点に集まる面の数が同じ
という2つの条件を満たす凸多面体のことであった。
以前、正多面体は5つしかないことの証明を書いた。
さて、先ほどの正多面体の条件を少し緩めたものを半生多面体と呼ぶ。
どのように緩めるかというと、先ほどの条件のうち、「すべての面が同じ」という条件をなくすのだが、すべての面が正多角形であるという条件は外さないままとする。
すると、先ほどの2条件は次のように置き換えられる:
半正多面体の条件(仮)
- すべての面が正多角形
- 1つの頂点に集まる面の数と種類が同じ
今度は、面がすべて同じではないので、2の条件も数が同じというだけではなく、数と種類が同じという条件に置き換わる。
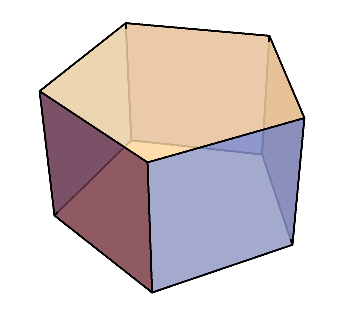
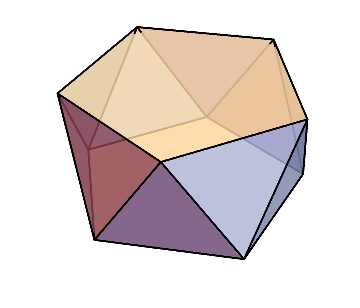
例えば、これは立方八面体と呼ばれる多面体だが、すべての頂点に対して、1つの頂点に2つの正三角形と2つの正方形が集まっている。
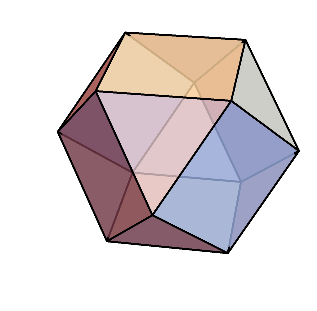
このように緩めた条件を満たす凸多面体を半生多面体と呼ぶ・・・と言い切れれば良かったのだが、実際にはある問題が生じる。
その問題とは、「半正多面体の条件(仮)」を満たす多面体が無限に存在してしまうことである。
以下の多面体を見てもらいたい。
これらは、五角柱と反五角柱である。
五角柱の場合、底面が正五角形、側面が正方形になるように辺の長さを調整すれば、1つの頂点に集まるのは正五角形1つと正方形2つになり、「半正多面体の条件(仮)」を満たしてしまう。
同様に、反五角柱の場合も、底面が正五角形、側面が正三角形になるようにすれば、1つの頂点に集まるのは正五角形1つと正三角形3つになり条件を満たす。
これの何が問題かと言うと、これが五角柱と反五角柱だけに限らないということである。
3以上のNについて、正N角柱と正反N角柱も、「半正多面体の条件(仮)」を満たすのである。
これによって、「半正多面体」は無限に存在することになってしまう。
別に無限に存在してても問題はないのだが、正多面体が5個しかないことを思うと、その拡張としての半正多面体も有限個であってほしい気もする。
ということで、角柱と反角柱は半正多面体の定義から例外として抜くことにしよう。
半正多面体の条件(改)
- すべての面が正多角形
- 1つの頂点に集まる面の数と種類が同じ
- ただし角柱と反角柱は除く
さて、半正多面体の定義はこれで良いだろうか?
実は、まだ少し気持ち悪い点が残っているのである。
これについては次回説明しよう。
今回はここまで!