菱形十二面体　その１０

これまでの記事

---

今回は、菱形十二面体の対称性に注目してみよう。

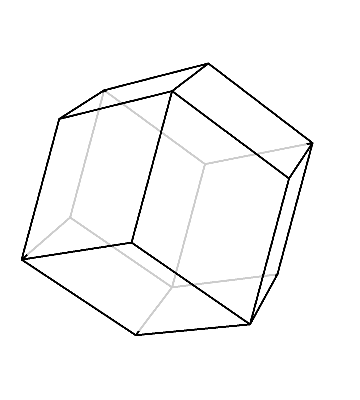
この菱形十二面体を、対称性の高い方向から見てみるとどうなるだろうか。

まず、菱形十二面体には、菱形の鋭角が4枚集まっている頂点と、菱形の鈍角が3枚集まっている頂点がある。

鋭角が4枚集まっている頂点の方向からまっすぐ見てみよう。

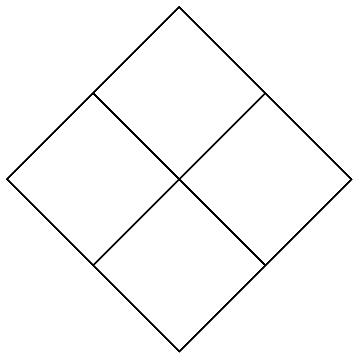
すると、菱形が4枚見えるはずだが、菱形を斜めから見ることになる影響で、菱形と言っても正方形型になる。

全体としても正方形の形をしている。

次に、鈍角が3枚集まっている頂点の方向からまっすぐ見てみる。

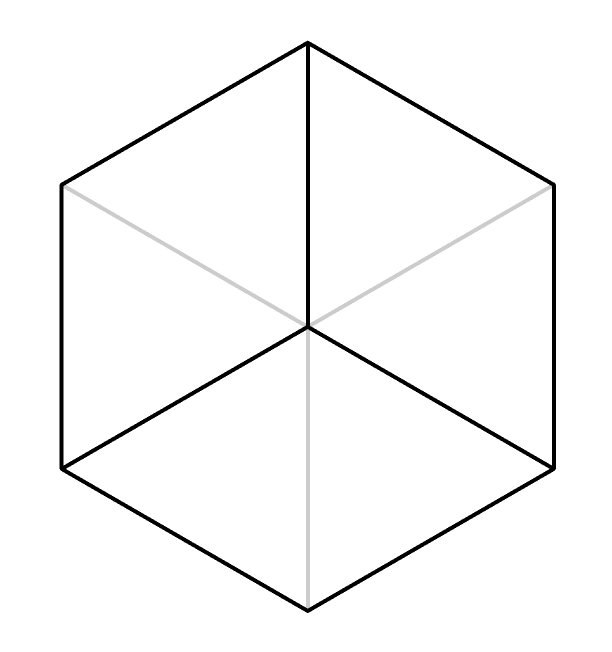
すると、菱形が3枚見えるのは予想通りだが、全体としては正六角形になる。

後ろが透けて見える場合は、正三角形が6枚集まった形になる。

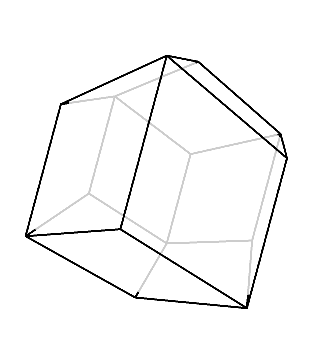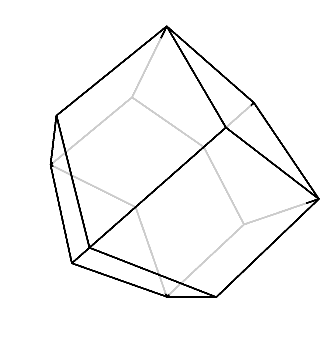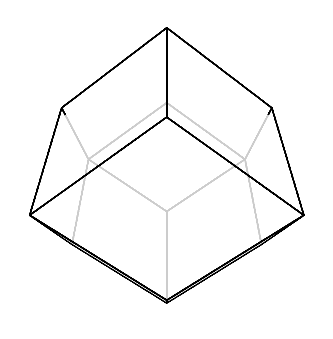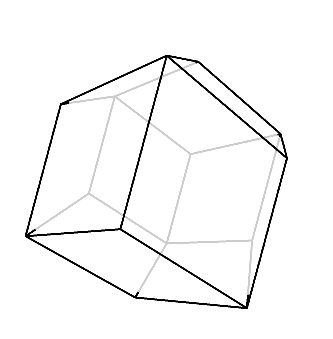
最後に、菱形が正面に見える方向から見てみよう。

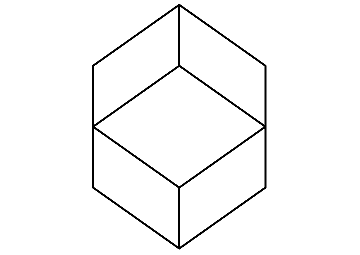
すると、このように正面の菱形の周りにある菱形が4枚、平べったくなりつつ見えていることが分かる。

以上の内容をgifアニメにしたのでぜひ見てもらいたい。