Science, Mathematics, Polyhedron, etc.
投稿日：
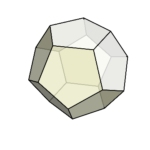
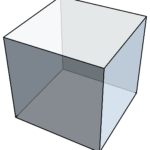
今回は、立方体から菱形十二面体を切り出す方法を紹介しよう。
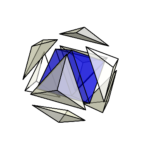
そのためには、立方体の各面からダイヤ型に切り出すことが必要になる。
以下でその様子を見ていく。
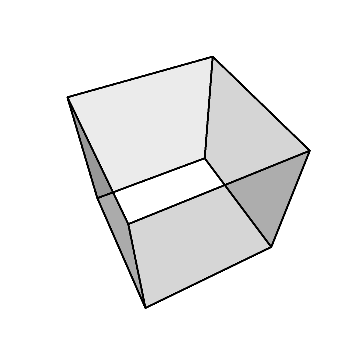
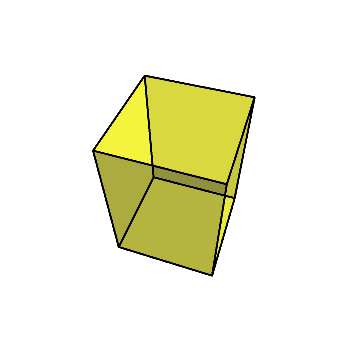
まず、立方体の面のうちの1つを上にして置き、そこからダイヤ型に切り出して、周りの部分は捨てる。
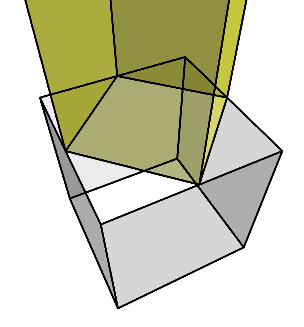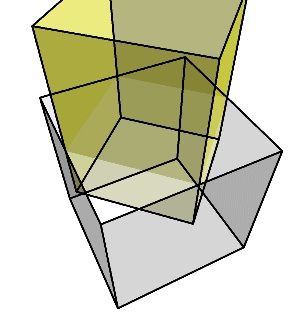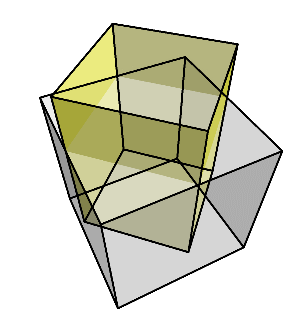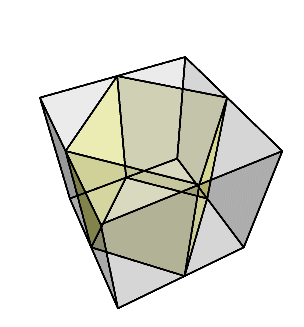
すると、下のように、少し細長い直方体が残る。
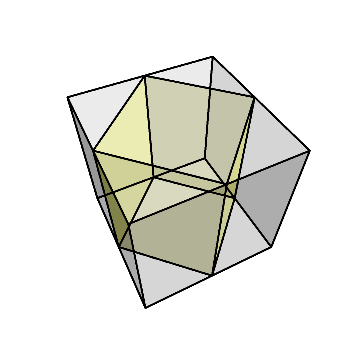
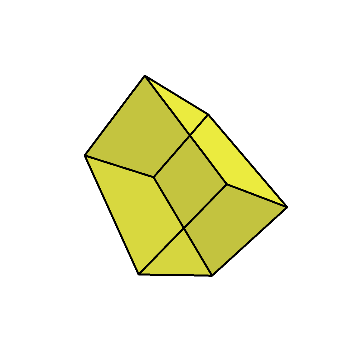
この直方体を上のように90度回して倒す。
そこに対して先ほどと同じようにダイヤ型に切り出す。
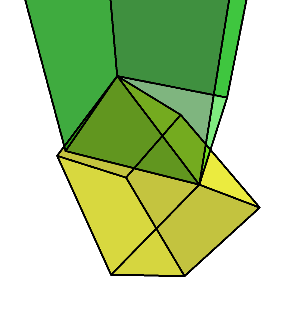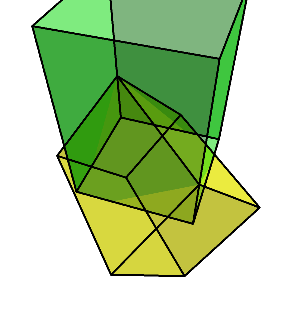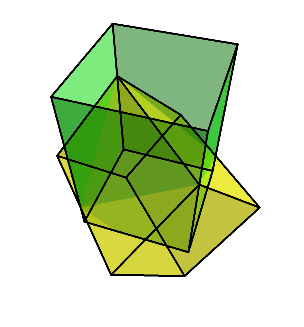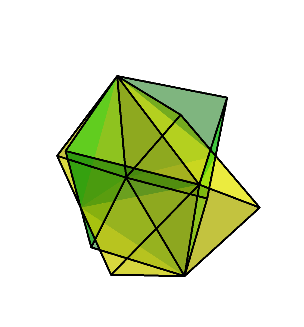
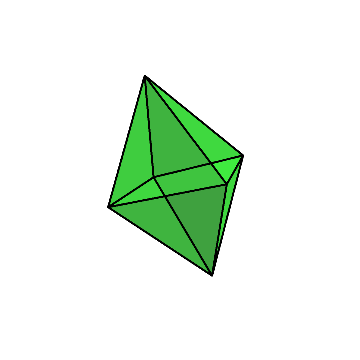
すると、下のように少し平べったい8面体が残る。
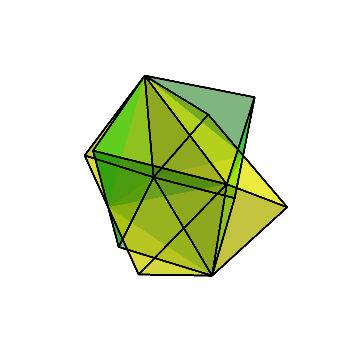
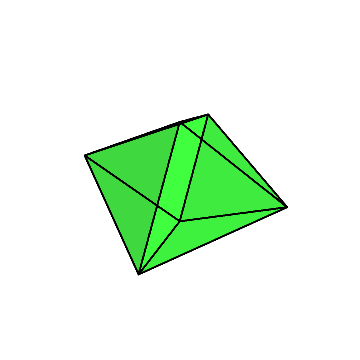
それをまた90度回して倒し、残った方向に対してダイヤ型に切り出す。
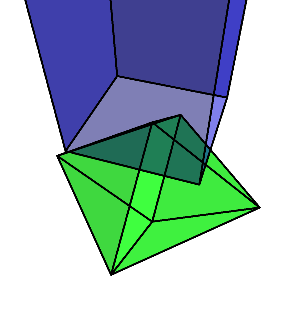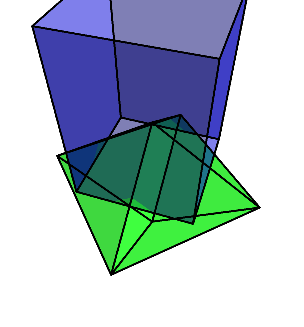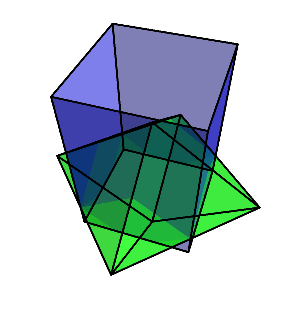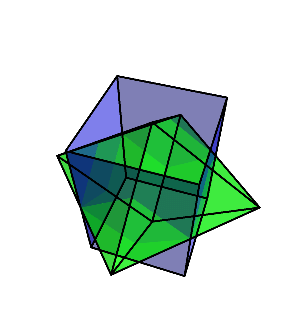
最終的に、菱形十二面体が残る。
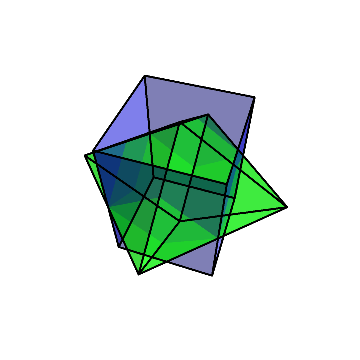
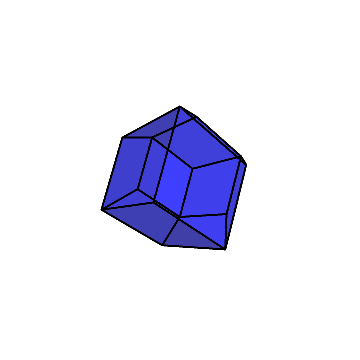
以上、立方体から菱形十二面体を切り出す方法を紹介した。
今回はここまで！
執筆者：epsilon
関連記事
これまでの記事 アユイ構成（Häuy Construction）という多面体の構成法がある。 この考案者のルネ＝ジュスト・アユイは、18世紀のフランスの鉱物学者で、「鉱物学の父」と呼ばれている。 アユ …
これまでの記事↓菱形十二面体菱形十二面体 その２菱形十二面体 その３菱形十二面体 その４菱形十二面体 その５ 今回も菱形十二面体の話をしよう。 今回は、菱形十二面体の各菱形の辺から中心に向かって切って …
今までに菱形十二面体の記事をたくさん書いてきたが、菱形十二面体についてどうしても書きたいことがある。 それは、「菱形十二面体は4次元立方体の射影である」という事実である。 しかし、これについて書くため …
これまでの記事 今回は、Mathematicaで領域をプロットする機能を使って菱形十二面体に関係する話をしよう。 Mathematicaには、不等号で表される領域をプロットするための関数が用意されてい …
前回、半正多面体の条件について考えた。 無限に存在する角柱と反角柱を半正多面体の対象から除くため、次のような条件にするのが良いのではないかというところまで書いた。 半正多面体の条件（改） すべての面が …
