Science, Mathematics, Polyhedron, etc.
投稿日：
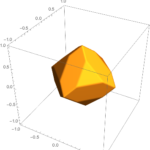
今回も菱形十二面体の話をしよう。
前回は、菱形十二面体の内部に立方体が隠れており、その残りの部分のピラミッドを6個集めると同じ大きさの立方体が組み上がることについて書いた。
今回は、内部の八面体以外の部分について同じようなことが可能かどうか見ていこう。
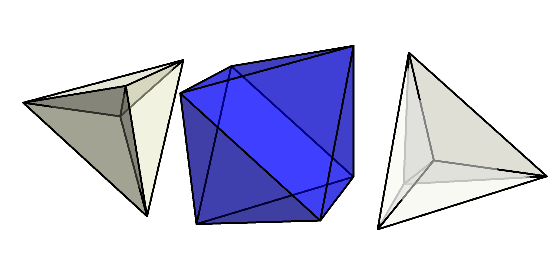
まず、菱形十二面体の中には正八面体も隠れているのだった。
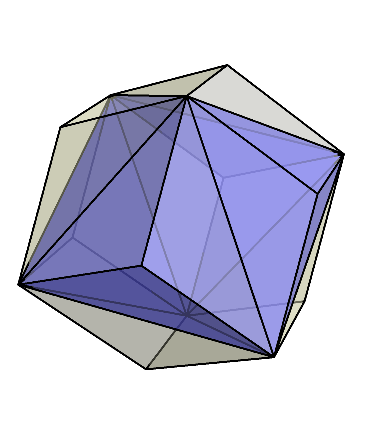
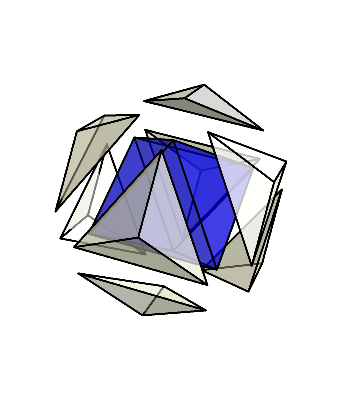
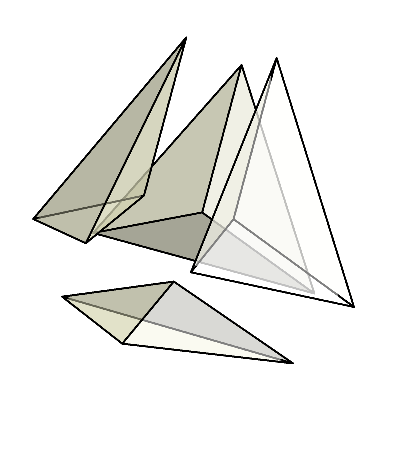
正八面体以外の部分は、平べったい三角錐になっている。
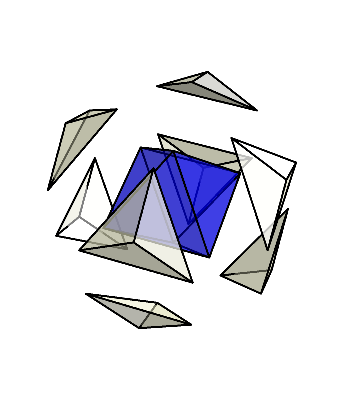
これらの三角錐のうち、4個だけ取り出して集めてみよう。
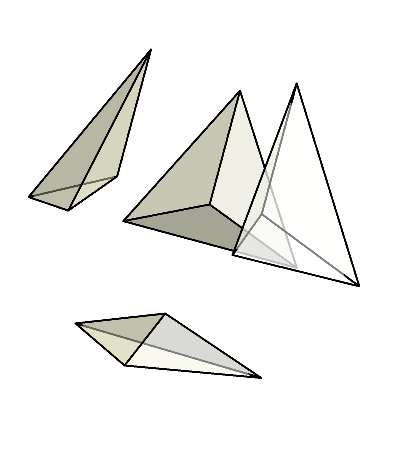
すると、今回は正四面体が現れる。
先ほど菱形十二面体をカットしたときに、平べったい三角錐は8個あったことを思い出すと、菱形十二面体1個から正八面体が1個と正四面体が2個作れることが分かる。
執筆者：epsilon
関連記事
これまでの記事 前回、アユイ構成という、立方体を使って多面体を近似するやり方を紹介した。
菱形十二面体菱形十二面体 その２菱形十二面体 その３菱形十二面体 その４ 今回も菱形十二面体の話をしよう。 その３で、菱形十二面体は立方体とピラミッド6個にカットできることを書いた。 このピラミッド6 …
これまでの記事 今回は、Mathematicaで領域をプロットする機能を使って菱形十二面体に関係する話をしよう。 Mathematicaには、不等号で表される領域をプロットするための関数が用意されてい …
これまでの記事↓菱形十二面体菱形十二面体 その２菱形十二面体 その３菱形十二面体 その４菱形十二面体 その５菱形十二面体 その６ 今回も菱形十二面体の話をしよう。 前回、菱形十二面体を各菱形の辺から中 …
