菱形十二面体　その７

これまでの記事↓
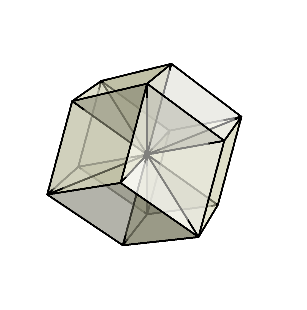
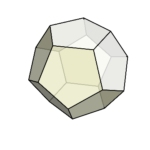
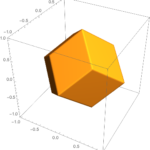
菱形十二面体
菱形十二面体　その２
菱形十二面体　その３
菱形十二面体　その４
菱形十二面体　その５
菱形十二面体　その６

---

今回も菱形十二面体の話をしよう。

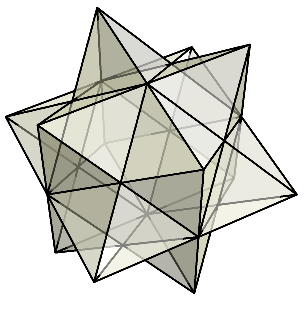
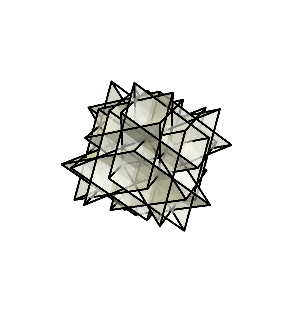
前回、菱形十二面体を各菱形の辺から中心に向かってカットしてできた菱形ピラミッドをひっくり返してくっつけると悪魔の星になるという話をした。

• 

• 

今回は、悪魔の星の菱形ピラミッドを中心に向かって押し込んでいくとどうなるか見てみよう。

中心に向かって押し込むと、当然、菱形ピラミッドどうしはぶつかるが、お互いを通り抜けるとして、押し込んでみる。

• 

• 

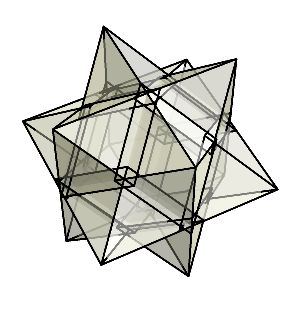
すると、悪魔の星の形は残っているが、どんどん小さくなっていくことが分かる。

十分押し込むと、このように元の半分の大きさの悪魔の星になる。

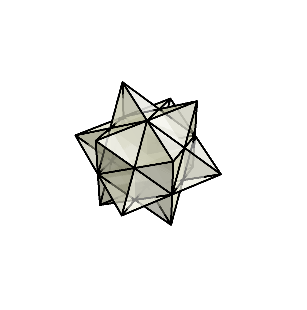
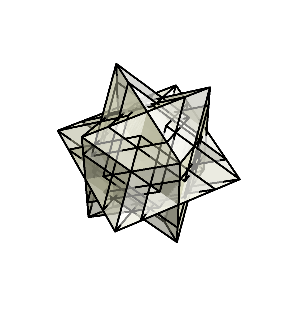
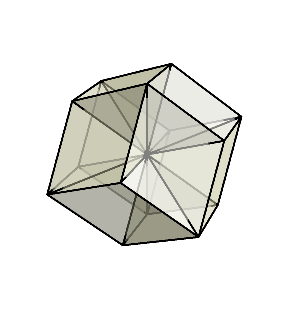
さらに押し込み続けてみよう。すると、反対側から菱形の面が出始めて、最終的に菱形十二面体が現れる。

• 

• 

ここまでの話は画像だけだとかなり分かりにくいと思うので、gifアニメを作ったのでぜひ見てもらいたい。

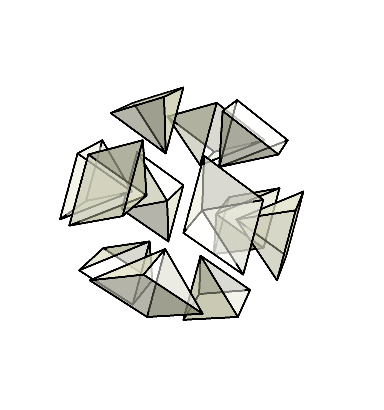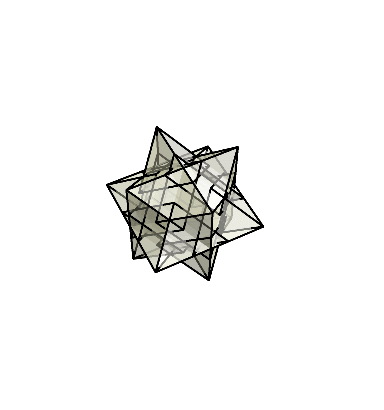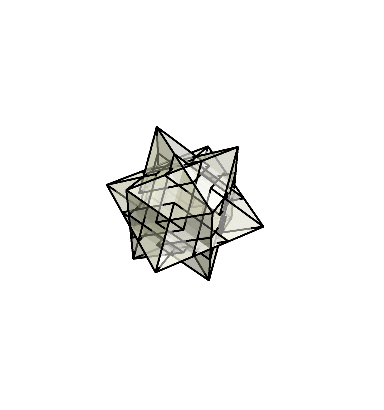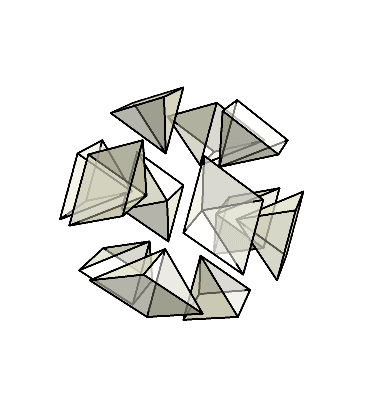
菱形十二面体と悪魔の星を行き来する様子が確認できただろうか。